Vídeos- aula : números irracionais

Números irracionais - o dilema dos matemáticos gregos

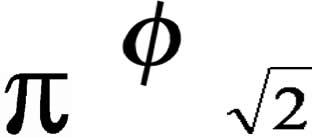
Um pouco de história...

Os matemáticos gregos antigos acreditavam que todos os problemas podiam ser resolvidos pelos números inteiros e números racionais.

No entanto, por volta de 400 a.C., resolvendo problemas geométricos, eles descobriram números que não eram inteiros e também não podiam ser escritos na forma de razão entre números inteiros. Isso os abalou muito – que tipo de número seriam aqueles ?

A origem histórica da necessidade de criação dos números irracionais está intimamente ligada com fatos de natureza geométrica e de natureza aritmética. Os de natureza geométrica podem ser ilustrados com o problema da medida da diagonal do quadrado quando comparamos com o seu lado.

Teorema de Pitágoras: “ A soma dos quadrados dos catetos é igual ao quadrado da

hipotenusa”.

Problema: Dado um quadrado de lado igual à unidade quanto mede a diagonal ?

A diagonal de um quadrado de lado medindo 1 é igual a √2.

Foi tentando resolver este problema usando o Teorema de Pitágoras que os gregos descobriram um “ novo” número: o número √2.

O Teorema de Pitágoras provocou, assim, a descoberta de novos números: os irracionais. Representam um marco importante para o pensamento humano, mas foi muito pertubadora para os pitagóricos.

Acredita-se que a descoberta desse números, que eles chamaram de “inexprimíveis”, e que hoje chamamos de números irracionais, tenha sido mantida em segredo durante certo tempo.

O número √2 é um número irracional, pois ao extrair sua raiz quadrada , obtemos o seguinte resultado: 1,414213562373... ( infinito e não-periódico ).

A raiz quadrada de 2 é portanto um dos números irracionais mais célebres. Se tentarmos calculá-la vemos que deve ser 1 e... alguma coisa! Mas a “ alguma coisa” é que é o problema ! Alguns matemáticos antigos iam perdendo também a razão a tentar descobrir essa “ alguma coisa”. O mais que apuraram, pobres deles, foi 17/12, que é 1 mais “ alguma coisa” ( 1 corresponde , como sabemos, a 12/12 ). Mas o quadrado de 17/12 é 289/144 ... E que

2 é ... 289/144!

Era “ quase” !

Ao encontrar os irracionais, aos quais não conseguem representar por uma razão entre dois inteiros m/n ( número racional ), os matemáticos gregos são levados a conceber grandezas incomensuráveis.

Outro número irracional muito usado na Geometria é o π ( pi ) descoberto por meio da divisão do comprimento de uma circunferência pelo diâmetro da mesma.

π = 3,141592653589793238462...

O número de Ouro ( divina proporção ) também é considerado um número irracional. O número "phi" representa o símbolo da harmonia. Os artistas gregos usavam-no em arquitetura; Leonardo da Vinci, nos seus trabalhos artísticos; e, no mundo moderno, o arquiteto Le Corbusier, com base nele, apresentou, em 1948, O modulor.

O número de ouro descobre-se em relações métricas:

• Na natureza: em animais ( como na concha do Nautilus ), flores, frutos, na disposição dos ramos de certas ár vores;
• Em figuras geométricas, tais como o retângulo de ouro, hexágono e decágono regulares e poliedros regulares;
• Em inúmeros monumentos, desde a Pirâmide de Quéops até diversas catedrais, na escultura, pintura e até na música.
  

Fonte de pesquisa:
http://www.mundoeducacao.com.br/matematica/numeros-irracionais.htm
http://www.somatematica.com.br/irracionais.php
http://sites.google.com/site/susymcmarques/historiadosnumerosirracionais
Livro didático: Novo Praticando Matemática - 7ª série
Autores: Álvaro Andrini e Maria José Vasconcellos

Probabilidade na loteria

Ganhar na loteria é o sonho de todo apostador, basta acertar os números sorteados. Frases como " só ganha quem joga" são ditas pelos apostadores convictos de embolsar os prêmios milionários oferecidos pelas loterias em todo país.
Mas você já pensou na probabilidade de acertar os números que são sorteados ?
Veja como calcular as chances de ganhar na mega sena e na quina.

Mega sena
A mega sena consiste num jogo de 60 números ( 1 a 60 ) no qual é permitido apostar de 6 a 15 números ( valor das apostas tende a aumentar conforme a quantidade de números assinalados por jogo ), podendo ganhar acertando 6 dezenas, 5 dezenas ou 4 dezenas, sendo que o prêmio principal é pago para quem acertar as 6 dezenas ( sena ), e proporcional para quem acertar 5 dezenas (quina ) ou 4 dezenas ( quadra ). A possibilidade de acerto das 6 dezenas é calculado aplicando uma combinação simples de 60 elementos tomados 6 a 6.

Lembrando que ! ( fatorial ) significa multiplicar o número por todos os seus antecessores naturais, com ausência do zero.Os cálculos nos mostram que existem 50.063.860 combinações possíveis. Por exemplo:
01 - 02 - 03 - 04 - 05 - 06
01 - 02 - 03 - 04 - 05 - 07
01 - 02 - 03 - 04 - 05 - 08
20 - 23 - 32 - 45 - 48 - 59
10 - 15 - 25 - 36 - 45 - 50
02 - 03 - 15 - 16 - 25 - 40

Se apostarmos 1 jogo de seis dezenas, a possibilidade de ganharmos é de 1 em 50.063.860, que corresponde a 0,000002% de chance de ganhar.

Quina
Na quina você pode apostar jogando 5, 6 ou 7 números ( valor da aposta tende a aumentar conforme a quantidade de números jogados ) dentre os 80 existentes.
Na quina a probabilidade de acerto de 5 dezenas também é calculada aplicando a definição de combinação simples , só que agora temos 80 números tomados 5 a 5.Então, se apostarmos 1 jogo de 5 dezenas , a probabilidade de ganhar é de 1 em 24.040.016, correspondente a 0,0000042% de chance de ganhar.

Fonte: http://www.mundoeducacao.com.br/matematica/probabilidade-na-loteria.htm

Sessão coletiva 4 _ TP2 Unidade 7

Nesta oficina trabalhamos com a matemática das incertezas. Sim, termos da linguagem cotidiana como: " é provável... ", " ao acaso...", " com certeza...", " qual é o risco ?" , " qual é a chance ?" , estão associados ao conceito matemático de probabilidade.
Os conceitos de probabilidade podem ser aplicados a várias situações de nosso dia a dia. Cabe ao professor de matemática trabalhar as noções informais e intuitivas que os alunos trazem para a sala de aula de forma a ajudá-lo a construir conhecimentos e fazer conexões mais ricas entre elas.
As atividades desenvolvidas nesta oficina foram: leitura de um texto contanto a história dos seguros , cálculo de probabilidades envolvendo furtos de veículos no Brasil, experimento com lançamento de moedas.

Transposição didática_ TP2 Unidade 8

As atividades desenvolvidas tinham por objetivo:

1. interpretação de dados a partir de um gráfico circular ou " gráfico de pizza";
2. favorecer a conexão entre valores percentuais e fracionários;
   
3. construção de gráfico circular através do compasso e por dobraduras;
4. identificar frações, graus e porcentagem em um gráfico circular sem o uso do tranferidor.

A situação-problema apresentada envolvia dados probabilísticos, conforme o tema trabalhado nesta unidade. A partir de então, foi promovida uma discussão para esclarecimento dos dados apresentados. Pode-se perceber uma maior facilidade dos alunos em compreenderem os dados como partes de um todo, pois conseguiram visualizar o círculo como um inteiro. O conceito foi reforçado quando os alunos trabalharam com cálculos envolvendo porcentagens e frações e suas correspondências ( em graus ) no gráfico circular. Esses cálculos puderam ser trabalhados mentalmente através das dobraduras no gráfico circular que eles reproduziram no papel.

Você já parou para pensar quanto mede a sua pele ?

Fique sabendo!

• a pele é o maior e mais visível órgão do corpo humano;
• ela representa 16% do peso do corpo humano. Parece pouco ? Em uma pessoa que tem 70 kg, a pele é responsável por cerca de 12 kg do seu peso;
• ela mede cerca de 2 metros quadrados, o equivalente a um retângulo de um metro de largura por dois de comprimento;
  
• pesa de 3 a 5 kg;
  
• ao longo da pele estão distribuídas 2 milhões de glândulas sudoríparas, responsáveis pela irrigação e desintoxicação da pele, por meio do suor. A maior concentração de glândulas está na palma das mãos: 370 por centímetro quadrado;
• as impressões digitais se formam ainda no útero, seis a oito semanas antes do nascimento da criança;
• é à prova d'água, lavável e elástica. Apesar de fica flácida ou enrugada quando envelhecemos , resiste surpreendentemente bem ao tempo.
  

Sessão Coletiva 3_ TP2 Unidade 5

Uma das atividades que foi desenvolvida nessa oficina estava relacionada a seguinte questão: Como você pode medir aproximadamente a sua superfície corporal ?
O grupo apresentou uma maneira prática para efetuar o cálculo: com muita criatividade foi criado um protótipo que pudesse reproduzir, aproximadamente, a superfície corporal de uma das participantes. A participante que serviu de " modelo" também dava suas sugestões de como essas medidas poderiam ser aferidas. Todo processo foi registrado no quadro de giz e através de fotografias. O método utilizado foi o cálculo de área de figuras planas a partir do modelo matemático para a situação-problema. Depois de todos os cálculos efetuados, o resultado final foi comparado ao apresentado na tabela de referência ( usada por médicos nefrologistas e cirurgiões plásticos ) e pôde-se constatar que os valores estavam bem próximos. Portanto, o modelo utilizado pelo grupo , apesar de não ser tão preciso, serviu de base para medição da superfície corporal de uma pessoa.