Vídeos- aula : números irracionais

Números irracionais - o dilema dos matemáticos gregos

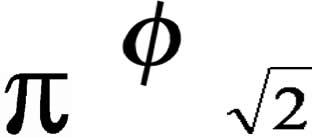
Um pouco de história...

Os matemáticos gregos antigos acreditavam que todos os problemas podiam ser resolvidos pelos números inteiros e números racionais.

No entanto, por volta de 400 a.C., resolvendo problemas geométricos, eles descobriram números que não eram inteiros e também não podiam ser escritos na forma de razão entre números inteiros. Isso os abalou muito – que tipo de número seriam aqueles ?

A origem histórica da necessidade de criação dos números irracionais está intimamente ligada com fatos de natureza geométrica e de natureza aritmética. Os de natureza geométrica podem ser ilustrados com o problema da medida da diagonal do quadrado quando comparamos com o seu lado.

Teorema de Pitágoras: “ A soma dos quadrados dos catetos é igual ao quadrado da

hipotenusa”.

Problema: Dado um quadrado de lado igual à unidade quanto mede a diagonal ?

A diagonal de um quadrado de lado medindo 1 é igual a √2.

Foi tentando resolver este problema usando o Teorema de Pitágoras que os gregos descobriram um “ novo” número: o número √2.

O Teorema de Pitágoras provocou, assim, a descoberta de novos números: os irracionais. Representam um marco importante para o pensamento humano, mas foi muito pertubadora para os pitagóricos.

Acredita-se que a descoberta desse números, que eles chamaram de “inexprimíveis”, e que hoje chamamos de números irracionais, tenha sido mantida em segredo durante certo tempo.

O número √2 é um número irracional, pois ao extrair sua raiz quadrada , obtemos o seguinte resultado: 1,414213562373... ( infinito e não-periódico ).

A raiz quadrada de 2 é portanto um dos números irracionais mais célebres. Se tentarmos calculá-la vemos que deve ser 1 e... alguma coisa! Mas a “ alguma coisa” é que é o problema ! Alguns matemáticos antigos iam perdendo também a razão a tentar descobrir essa “ alguma coisa”. O mais que apuraram, pobres deles, foi 17/12, que é 1 mais “ alguma coisa” ( 1 corresponde , como sabemos, a 12/12 ). Mas o quadrado de 17/12 é 289/144 ... E que

2 é ... 289/144!

Era “ quase” !

Ao encontrar os irracionais, aos quais não conseguem representar por uma razão entre dois inteiros m/n ( número racional ), os matemáticos gregos são levados a conceber grandezas incomensuráveis.

Outro número irracional muito usado na Geometria é o π ( pi ) descoberto por meio da divisão do comprimento de uma circunferência pelo diâmetro da mesma.

π = 3,141592653589793238462...

O número de Ouro ( divina proporção ) também é considerado um número irracional. O número "phi" representa o símbolo da harmonia. Os artistas gregos usavam-no em arquitetura; Leonardo da Vinci, nos seus trabalhos artísticos; e, no mundo moderno, o arquiteto Le Corbusier, com base nele, apresentou, em 1948, O modulor.

O número de ouro descobre-se em relações métricas:

• Na natureza: em animais ( como na concha do Nautilus ), flores, frutos, na disposição dos ramos de certas ár vores;
• Em figuras geométricas, tais como o retângulo de ouro, hexágono e decágono regulares e poliedros regulares;
• Em inúmeros monumentos, desde a Pirâmide de Quéops até diversas catedrais, na escultura, pintura e até na música.
  

Fonte de pesquisa:
http://www.mundoeducacao.com.br/matematica/numeros-irracionais.htm
http://www.somatematica.com.br/irracionais.php
http://sites.google.com/site/susymcmarques/historiadosnumerosirracionais
Livro didático: Novo Praticando Matemática - 7ª série
Autores: Álvaro Andrini e Maria José Vasconcellos